This week I read papers that blows my mind. I write this blog to share my understanding about Lottery Ticket Hypothesis. As always, suggestions and corrections are always welcome 😃
Drawing Winning Tickets
Model pruning is a commonly used practice to reduce the number of parameters in a model while still maintaining performance. The question is, if a smaller model with fewer parameters can achieve good evaluation results, why do we need to train the entire model? Wouldn’t it be faster and cheaper to only train the smaller portion of the model in isolation? This smaller portion of the model is referred to as “winning tickets” because these portions “win” the random weight initialization lottery. I personally love these terms.
So, how do we identify these winning tickets? Through pruning, we can naturally uncover these powerful subnetworks. The Lottery Ticket Hypothesis states that there exists a mask $m \in {0,1}$, for which $j’ \leq j$ (with commensurate training time), $a’ \geq a$ (with commensurate accuracy), and $||m||_{0} \ll |\theta|$ (with fewer parameters), where $j$ represents the iteration, $a$ represents accuracy, $\theta$ represents parameters, and the accent denotes a pruned version.
The Algorithm
In [1], the author proposes two methods for finding winning tickets: one-shot pruning and iterative pruning. The one-shot pruning method is more intuitive, so let’s start with that. The algorithm proceeds as follows:
- Randomly initialize the network with parameters $f(x;\theta_{0})$.
- Train for $j$ iterations until reaching parameter $\theta_j$.
- Prune $p$% of the parameters, creating a mask $m$.
- Reset the remaining parameters to $\theta_0$ and create the winning ticket $f(x; m \odot \theta_0)$.
On the other hand, the iterative pruning algorithm follows these steps:
- Randomly initialize the network with parameters $f(x;\theta_{0})$.
- Train for $j$ iterations until reaching parameter $\theta_j$.
- Prune $p^{\frac{1}{n}}$% of the parameters, creating a mask $m$.
- Reset the remaining parameters to $\theta_0$ and create the winning ticket $f(x; m \odot \theta_0)$.
- Repeat these steps for $n$ rounds.
Both algorithms, especially iterative pruning, can be computationally expensive since they require fully training the network to find the winning ticket.
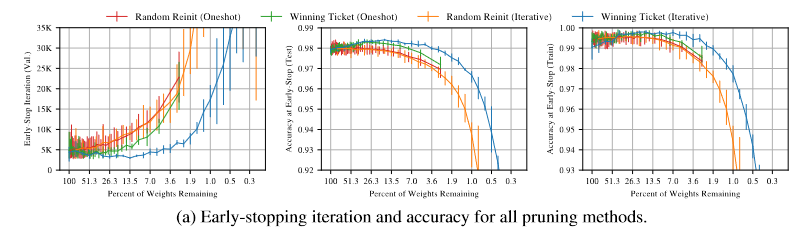
From figure above, winning ticket obtained by iterative pruning (blue line) is much better than winning ticket obtained by one-shot (green) since it’s stop earlier and having better accuracies for both train and test dataset.
Why is this works?
The author of the study then investigates why winning tickets are able to match or even outperform the performance of the full network. They observe the connectivity between the importance of the winning ticket initialization and the success of the sparse-structured network on which the winning ticket is applied.
The Importance of Winning Ticket Initialization
It turns out that a winning ticket architecture without the exact same initialization weights will make the network learn slower. This indicates the importance of the winning ticket initialization. The author argues that the possible explanation is that the initial weights are already close to the final weights or, in extreme cases, the initial weights may have already been trained. Empirically, the author shows that the winning ticket weights move further away than other weights, which means that the initial winning ticket weights are connected to the optimization algorithm, dataset, and model.
The Importance of Winning Ticket Structure
The structure of winning tickets is important in the Lottery Ticket Hypothesis. Winning tickets are subnetworks of a larger neural network that are capable of achieving similar or better performance with far fewer parameters. The hypothesis suggests that these subnetworks exist within larger networks and can be uncovered by applying a pruning technique to remove the unnecessary parameters.
The structure of winning tickets is important because it determines which subset of the network’s parameters is necessary for achieving good performance. Identifying the winning ticket structure can lead to the creation of smaller and more efficient models that can perform as well as larger models.
The author proposes a hypothesis that the structure of the winning ticket encodes an inductive bias that is tailored to the specific learning task. This allows the model to retain its ability to learn even after undergoing heavy pruning.
Lottery Ticket Hypothesis Limitation
In the research paper [1], the author solely conducted experiments on classification tasks centered around visual data and did not explore the effectiveness of pruning on larger datasets. Despite producing a sparse network, the resulting architecture may not be optimized for certain modern libraries or hardware.
For deeper networks like ResNet and VGG, the iterative pruning method is unable to uncover winning tickets unless the network is trained with a learning rate warmup. It is not yet clear why this warmup process is necessary, but the research suggests that it could potentially help the network reach a more optimal solution. Overall, further research is needed to fully understand the effectiveness of pruning and its implications on various types of models and datasets.
Early-Bird Tickets
Winning tickets are amazing! but I think the main drawback is the proposed way to identify it is pretty costly. Turns out, [2] reveals that winning ticket is able to be identified in early stage of training. This “early” winning ticket is callled Early-Bird Ticket or EB Ticket for short. I love how they named it 😄. The main idea is to prune the network at earlier points.
The question is whether EB Tickets always exist. To investigate, the author conducted an experiment with different learning rate schedulers. They used an initial learning rate of 0.1, which was divided by 10 at different epochs. The first experiment divided it at 80th and 120th epochs, denoted as $[80, 120]$, while the second option divided it at epoch 0 and 100, denoted as $[0, 100]$.
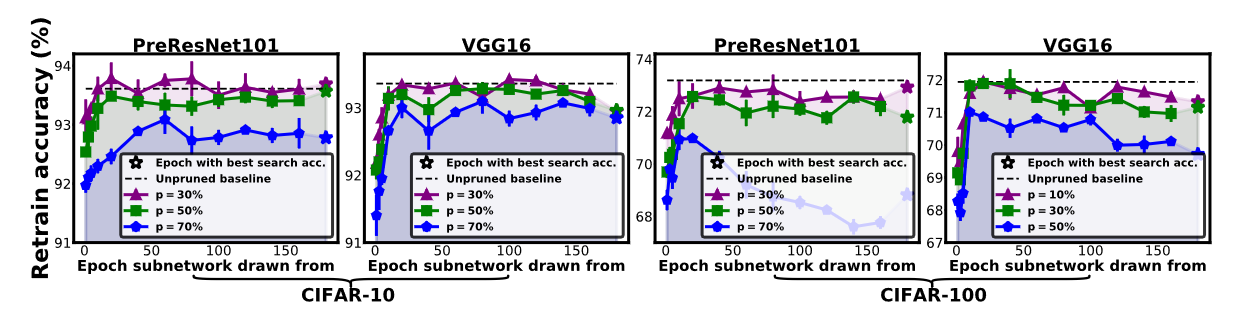
Figure above shows that there consistently exist EB ticket that drawn at earlier epoch ranges, that outperform their unpruned/original model. Potentially, this because of sparse regularization that make the pruned model more generalize. Figure above also shows that over-pruning ($p \geq 70$%) is hurting the performance.
Low Cost Training
The author also tests the performance of the network in a low-cost training environment, which involves using a high learning rate and low precision training. The scores obtained from the different learning rate schedulers are presented below.
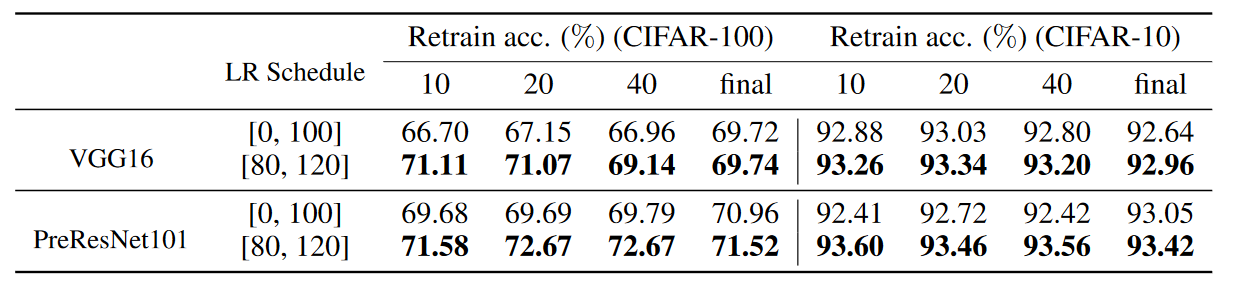
Turns out, $[80, 120]$ is better than $[0, 100]$. This shows that larger learning rate (since the learning rate is decayed on later epoch) is still able to uncovers high quality EB ticket with higher accuracy score .
In addition, the author tests the network’s performance under low-precision training conditions, where model weights, activation functions, gradients, and errors are quantized to 8 bits to improve training time efficiency. Note that quantization is only applied when identifying EB tickets, after which the tickets are trained on full precision. Remarkably, EB tickets still emerge even under these aggressive low-precision training conditions.
The Algorithm
The author proposes a method called EBTrain to determine when to stop training and prune the model by using mask distance, specifically hamming distance, to identify the emergence of EB tickets. To do this, they measure the mask distance between epochs, and if the highest distance of the last five recorded mask distances is less than a certain threshold $\epsilon$, they stop training since an EB ticket has been found. They calculate and normalize the mask distances to visualize the rate of change in mask distance presented below.
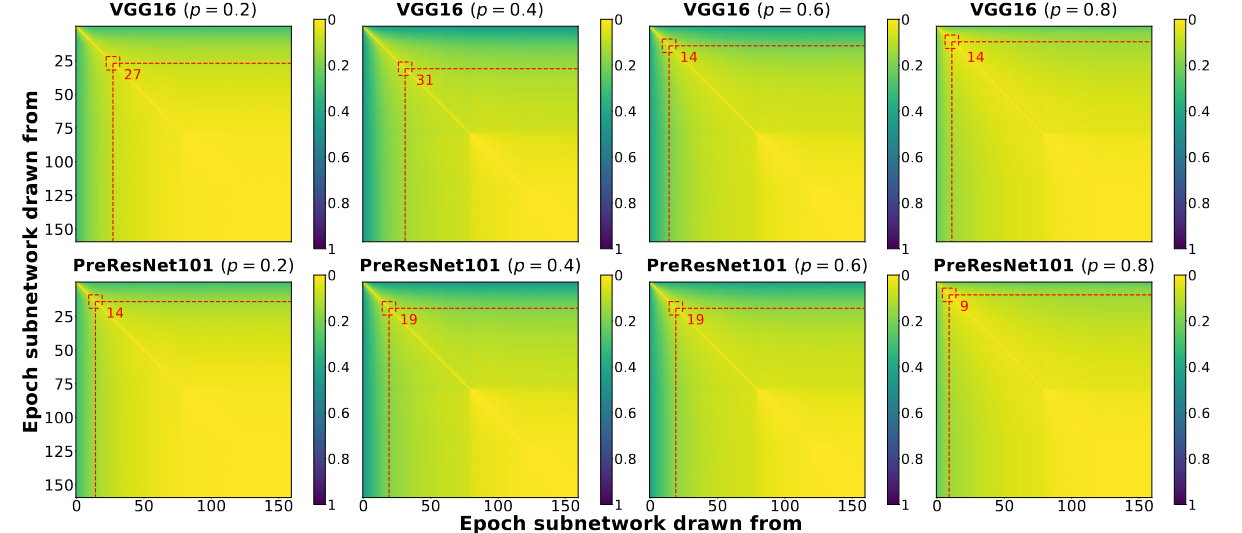
Figure above shows that the mask distance is approaching to 0 (yellow) in later epochs. This means that there’s not much mask changes is later epochs. This visualization strengthen the emergence of EB tickets.
EBTrain uses a FIFO queue to record mask distance and inherits unpruned weights from the drawn EB tickets instead of rewinding to the original initialization. This approach enables EBTrain to achieve a 2.2 to 2.4 times reduction in FLOPs (floating point operations) compared to the original baseline, while maintaining comparable or even better accuracy.
That’s it! Thank you for reading my blog post. Please let me know what you think of this amazing discovery! 🤗
References
[1] https://arxiv.org/abs/1803.03635v5
[2] https://arxiv.org/abs/1909.11957v5